Le indagini geosismiche sono state realizzate avvalendosi del metodo sismico che utilizza l’acquisizione del rumore sismico di fondo come funzione di eccitazione.
Il rumore sismico, generato dai fenomeni atmosferici (onde oceaniche, vento) e dall’attività antropica, è presente ovunque sulla superficie terreste, si chiama anche microtremore poiché riguarda oscillazioni molto più piccole di quelle indotte dai terremoti nel campo prossimo all’epicentro.
I microtremori sono solo in parte costituiti da onde di volume, P o S. In essi giocano un ruolo fondamentale le onde superficiali, che hanno velocità prossime a quella delle onde S (vedi ad es. Lachet e Bard, 1994), il che spiega la dipendenza di tutta la formulazione dalla velocità di queste ultime. Dai primi studi di Kanai (1957) in poi, diversi metodi sono stati proposti per estrarre l’informazione relativa al sottosuolo dal rumore sismico registrato in un sito. Tra questi, la tecnica che si è maggiormente consolidata nell’uso è quella dei rapporti spettrali tra le componenti del moto orizzontale e quella verticale (Horizontal to Vertical Spectral Ratio, HVSR o H/V), proposta da Nogoshi e Igarashi (1970). La tecnica è universalmente riconosciuta come efficace nel fornire stime affidabili della frequenza fondamentale di risonanza del sottosuolo (Field e Jacob, 1993; Lachet e Bard, 1994; Lermo e Chavez-Garcia, 1993, 1994; Bard, 1998; Ibs-von Seht e Wohlenberg, 1999; Fah et al., 2001; solo per citarne alcune).
Le basi teoriche dell’H/V sono relativamente facili da comprendere in un mezzo del tipo strato + bedrock (o strato assimilabile al bedrock) in cui i parametri sono costanti in ciascuno strato. Considerando un sistema in cui gli strati 1 e 2 si distinguono per le diverse densità (r1e r2) e le diverse velocità delle onde sismiche (V1 e V2), un’onda che viaggia nel mezzo 1 viene (parzialmente) riflessa dall’interfaccia che separa i due strati. L’onda così riflessa interferisce con quelle incidenti, sommandosi e raggiungendo le ampiezze massime (condizione di risonanza) quando la lunghezza dell’onda incidente (l) è 4 volte (o suoi multipli dispari) lo spessore H del primo strato. La frequenza fondamentale di risonanza (fr) dello strato 1 relativa alle onde S è pari a fr= Vs1/4H (1)
Questo effetto è sommabile, anche se non in modo lineare e senza una corrispondenza 1:1, ciò significa che la curva H/V relativa ad un sistema a più strati contiene l’informazione relativa alle frequenze di risonanza (e quindi allo spessore) di ciascuno di essi, ma è interpretabile attraverso opportuni fattori di correlazione.
L’analisi H/V permette pertanto di identificare i contrasti di impedenza tra strati, la successiva determinazione della velocità delle onde S fino a profondità notevoli (ben oltre i 100 m di profondità) e strettamente dipendenti dallo spazio temporale di acquisizione; quindi l’elaborazione del Vs30, avviene attraverso una formulazione specifica adottando come punto di partenza la relazione (1) mostrata in precedenza.
Per i nostri scopi, la determinazione delle onde di taglio (onde S) entro i primi 30 metri di spessore ha permesso di definire il parametro Vs30 e di poter altresì caratterizzare i terreni in esame ai sensi dell’ Ordinanza 3274 – Nuova Normativa Antisismica del 20/03/2003, richiamata successivamente dal DM 14/01/2008.
ESEMPIO DI REPORT DI PROVA
Start recording: 17/05/10 17:40:11 End recording: 17/05/10 18:00:12
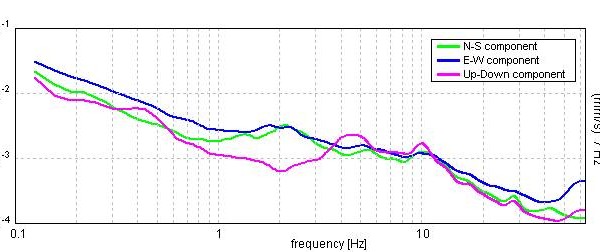
Channel labels: NORTH SOUTH; EAST WEST ; UP DOWN;
GPS data not available;
Trace length: 0h20’00”. Analyzed 98% trace (manual window selection);
Sampling frequency: 128 Hz;
Window size: 20 s;
Smoothing window: Triangular window;
Smoothing: 10%
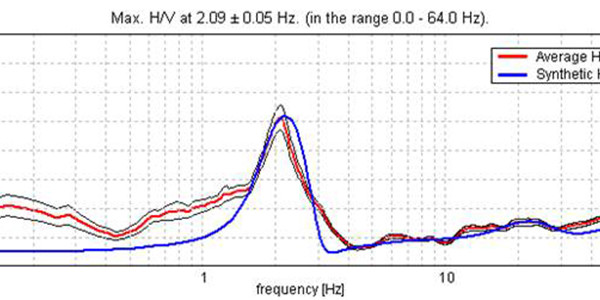
EXPERIMENTAL VS. SYNTHETIC H/V
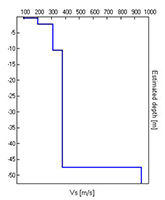
| Depth at the bottom of the layer [m] | Thickness [m] | Vs [m/s] |
| 0,50 | 0,50 | 100 |
| 2,30 | 1.80 | 200 |
| 10.60 | 8.30 | 310 |
| 47.60 | 37.00 | 380 |
| inf. | inf. | 950 |
According to the Sesame, 2005 guidelines. Please read carefully the Grilla manual before interpreting the following tables.]
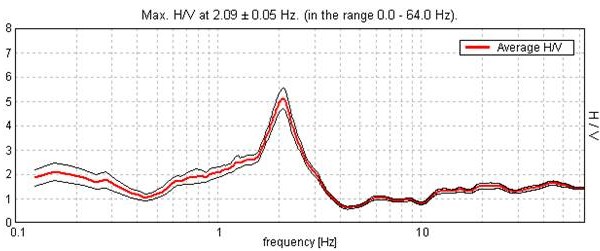
| Max. H/V at 2.09 ± 0.05 Hz. (in the range 0.0 – 64.0 Hz). |
| Criteria for a reliable HVSR curve
[All 3 should be fulfilled] |
| f0 > 10 / Lw | 2.09 > 0.50 | OK |
| nc(f0) > 200 | 2470.6 > 200 | OK |
| sA(f) < 2 for 0.5f0 < f < 2f0 if f0 > 0.5Hz
sA(f) < 3 for 0.5f0 < f < 2f0 if f0 < 0.5Hz |
Exceeded 0 out of 102 times | OK |
Criteria for a clear HVSR peak
[At least 5 out of 6 should be fulfilled]
|
Exists f – in [f0/4, f0] | AH/V(f –) < A0 / 2 |
1.344 Hz |
OK |
|
Exists f + in [f0, 4f0] | AH/V(f+) < A0 / 2 |
2.719 Hz |
OK |
|
A0 > 2 |
5.12 > 2 |
OK |
|
fpeak[AH/V(f) ± sA(f)] = f0 ± 5% |
|0.01102| < 0.05 |
OK |
|
sf < e(f0) |
0.02308 < 0.10469 |
OK |
|
sA(f0) < q(f0) |
0.2134 < 1.58 |
OK |
|
Threshold values for sf and sA(f0) |
|||||
|
Freq.range [Hz] |
< 0.2 |
0.2 – 0.5 |
0.5 – 1.0 |
1.0 – 2.0 |
> 2.0 |
|
e(f0) [Hz] |
0.25 f0 |
0.2 f0 |
0.15 f0 |
0.10 f0 |
0.05 f0 |
|
q(f0) for sA(f0) |
3.0 |
2.5 |
2.0 |
1.78 |
1.58 |
|
Log q(f0) for slogH/V(f0) |
0.48 |
0.40 |
0.30 |
0.25 |
0.20 |